Lab 8 - FIR

ECG

O sinal ECG gerado no pino PB13 possui a forma de onda a seguir:

E se analisarmos o espectro do sinal via transformada de fourier, obtemos a seguinte composição espectral:

60 Hz

Notamos claramente que existe um sinal centrada em 60Hz, isso é muito comum quando trabalhamos com eletrônica e reflete o 60Hz da rede elétrica que é propagada de diversas formas para o transdutor responsável em amostrar o dado do pulso elétrico do corpo humano, causando um ruído no sinal não desejável.

Para trarmos o dado corretamente teremos que filtar o ruído. Lembre que em alguns paises a frequência da rede elétrica é de 50Hz e não de 60Hz como no Brasil.

Filtros digitais

Filtragem de sinal pertence a uma grande área do conhecimento que é processamento de sinais, nesse laboratório iremos tratar do tema de forma superficial. Mas exemplos de aplicação de filtragem digital são:

• Remoção de ruído
• Processamento de Áudio
• Extração de parâmetros
• ...

FIR

O Finite Impulse Response (FIR) é uma técnica de processamento digital de sinais (DSP) que é capaz de realizar filtragens em um sinal. Com o FIR somos capazes de aplicar um filtro do tipo:

• passa baixas: Elimina as altas frequências
• passa altas: Elimina as baixas frequências
• mata faixa: Elimina uma faixa de frequências do sinal

Filtros digitais do tipo FIR possuem as seguintes vantagens:

1. São estáveis por natureza (não importa o parâmetro do filtro, o sinal de saída vai ser estável)
2. Podem ser projetados para ter fase linear
3. Possuem flexibilidade no seu projeto
4. São fáceis de implementar

O filtro possui a seguinte estrutura:

$$y[n] = b_0*x[n] + b_1*x[n-1] + .... b_n*x[n-N]$$

Onde:

• $y[n]$: Valor filtrado
• $x[n-N]$: Valor do dado não filtrado, atrasado de N amostras
• $b_n$: Coeficiente do filtro
• $N$: Ordem do filtro

Podemos representar a equação graficamente:

Fonte: https://en.wikipedia.org/wiki/Finite_impulse_response

• $Z^{-1}$: Significa um atraso na amostra

Projeto do filtro

Podemos realizar o projeto do filtro FIR (achar a ordem N e os coeficientes B) de diversas maneiras diferentes, cada um possui uma vantagem sobre a outra. Vamos utilizar o Equiripple Algorithm que possui ripples em torno da frequência de corte (fc).

Fonte: https://www.recordingblogs.com/wiki/equiripple-filter

O projeto do filtro envolve vários parâmetros e diversas escolhas, vamos verificarmos os mais importantes:

• $f_s$: Frequência de amostragem do sinal
• $f_c$: Frequência de corte, quando a componente espectral já possui um ganho baixo e não influencia 'tanto' no sinal. Na $f_c$ o ganho do sinal é geralmente -3dB, o que significa em volts, que o sinal possui $sqrt(½)=0.707$ do seu valor inicial.

pyfda

Para o projeto do filtro vamos utilizar uma ferramenta em python pyfda que vai nos ajudar encontrar os coeficientes b e N do filtro. Para isso siga os passos de instalação a seguir:

git clone https://github.com/chipmuenk/pyFDA/
cd pyFDA
pip3 install -r requirements.txt --user
python3 -m pyfda.pyfdax

Configure o filtro para:

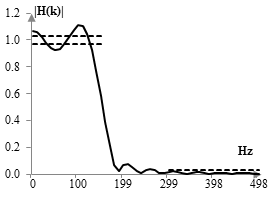
E agora clique em DESIGN FILTER. Vá na aba b,a e salve os valores de b em um txt, vamos usar mais tarde !

firmware

Esse exemplo possui:

• task_mxt: Leitura do touch
• task_lcd: Para exibição dos dados no LCD
• task_adc: Inicia um TC para fazer a conversão do ADC, recebe o dado e envia por uma fila.
• TC1: Timer configurado em 50Hz para fazer gerar o trigger da conversão analógica
• AFEC: Para realizar a leitura do potenciometro

Plotando ADC no tempo

Vamos modificar a task_lcd para exibir o valor da leitura do potenciometro no tempo. O resultado esperado é o seguinte:

Agora você deve modificar o plot, para plotar além do plot.raw exibir o plot.filtrado que mais para frente no lab será o nosso dado do ADC filtrado com o filtro projetado anteriormente. Atualmente ele é o valor plot.raw deslocado de 100.

ili9488_set_foreground_color(COLOR_CONVERT(COLOR_RED));

Filtrando dado

Vamos agora aplicar o filtro projetado anteriormente no dado adc, iremos utilizar uma biblioteca da ARM chamada de CMSIS DSP 4 que possui uma série de funções matemáticas e de processamento de sinais. Dentro dessa biblioteca, iremos utilizar a função arm_fir_init_f32 e arm_fir_f32 que respectivamente: inicializa o filtro FIR do tipo float_32 e aplica o filtro (convolução) ao sinal.

Inicializando filtro

Crie os defines a seguir:

#define NUM_TAPS   8  // ordem do filtro (quantos coefientes)
#define BLOCK_SIZE 1   // se será processado por blocos, no caso não.

Agora vamos copiar os coeficientes do filtro que foram gerados na etapa do projeto do filtro para a variável firCoeffs32:

const float32_t firCoeffs32[NUM_TAPS] ={0.12269166637219883,
    0.12466396327768503,
    0.1259892807712678,
    0.12665508957884833,
    0.12665508957884833,
    0.1259892807712678,
    0.12466396327768503,
  0.12269166637219883};

Agora dentro da task_adc (apos o TC_ini), vamos iniciar o filtro:

/* Cria buffers para filtragem e faz a inicializacao do filtro. */
float32_t firStateF32[BLOCK_SIZE + NUM_TAPS - 1];
float32_t inputF32[BLOCK_SIZE + NUM_TAPS - 1];
float32_t outputF32[BLOCK_SIZE + NUM_TAPS - 1];
arm_fir_instance_f32 S;
arm_fir_init_f32(&S, NUM_TAPS, (float32_t *)&firCoeffs32[0], &firStateF32[0], BLOCK_SIZE);

Processando

Modifique o while da task adc para realizar a filtragem e enviar para o LCD exibir.

int i = 0;

while(1){

if (xQueueReceive( xQueueADC, &(adc), 100)) {
        if(i <= NUM_TAPS){
          inputF32[i++] = (float) adc.value;
        } else{
          arm_fir_f32(&S, &inputF32[0], &outputF32[0], BLOCK_SIZE);
          plot.raw = (int) inputF32[0];
          plot.filtrado = (int) outputF32[0];
          xQueueSend(xQueuePlot, &plot, 0);
          i = 0;
        }

Resultado esperado:

B

• Criar um novo filtro de ordem 12 e trocar o atual

A

No lugar de mostrar uma linha no tempo, fazer um ponto em um circulo