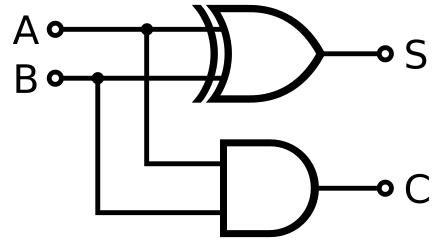• Teoria

Aritmética Binária - HW

  • Conteúdo: hald-adder/ full-adder/ somador

Tip 1

Esse conteúdo está no cap. 2 do livro texto da disciplina The Elements of Computing Systems.

Precisamos lembrar que nosso objetivo principal é a criação de um hardware capaz de operar com números binários. Nessa teoria iremos analisar algumas técnicas de realizar o hardware necessário para realizar operação de soma binária entre dois vetores. Para isso iremos definir dois componentes: Half-Adder e o Full-Adder.

half-adder (HAD)

Half-Adder (HAD) é um circuito digital capaz de somar dois bits (a e b), tem como resultado o valor da soma e do carry, como ilustrado a seguir: 

        ------
  a -->|      |--> Soma
       |  HA  |
  b -->|      |--> Carry
        ------

O HAD possui a seguinte tabela verdade:

a b Carry (out) Soma (out)
0 0 0 0
0 1 0 1
1 0 0 1
1 1 1 0

E é implementado em hardware da seguinte maneira:

Fonte: https://en.wikipedia.org/wiki/Adder_(electronics)

full-adder (FAD)

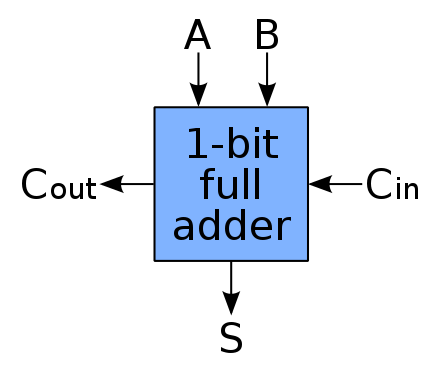
Full-adder é um componente digital capaz de somar três vits (a, b e c) e possui como saída o valor da soma e do carry resultante da operação. A seguir um diagrama de blocos de um FAD:

Fonte: https://en.wikipedia.org/wiki/Adder_(electronics)

O FAD possui a seguinte tabela verdade:

a b c Carry (out) Soma (out)
0 0 0 0 0
0 0 1 0 1
0 1 0 0 1
0 1 1 1 0
1 0 0 0 1
1 0 1 1 0
1 1 0 1 0
1 1 1 1 1

E é implementado da seguinte maneira em portas lógicas:

Fonte: https://en.wikipedia.org/wiki/Adder_(electronics)

Tip 2

Você deve ser capaz de encontrar esses circuitos analisando a tabela verdade e simplificando via Mapa de K.

Note que existem duas abordagens para representar o Carry_out: A.B+A.C+B.Ce A.B+C(A xor B)

Fonte: (2011) Fundamentals of Digital and Computer Design with VHDL, pg 199.

Somador

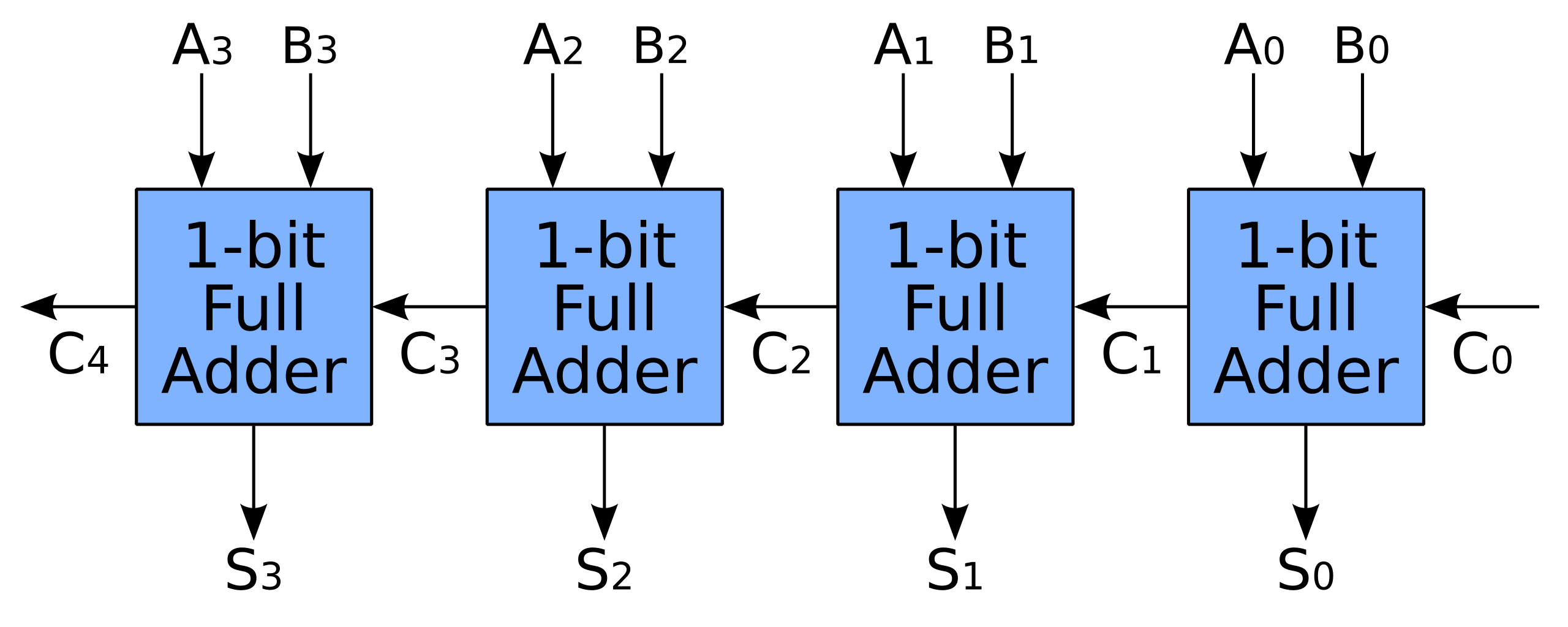
Utilizando o FAD somos capazes de realizar um somador de dois vetores binários. Para isso, teremos que utilizar um full-adder para cada bit desse nosso vetor.

Por exemplo: se formos criar um Somador capaz de somar dois vetores de 4bits, necessitamos utilizar 4 FAD para isso com a ligação descrita a seguir:

Fonte: https://en.wikipedia.org/wiki/Adder_(electronics)

Nesse diagrama, estamos realizando a soma ente os vetores A(3 downto 0) e B(3 downto 0) que resulta em um outro vetor S(3 downto 0) e um carry C4.