Efeitos colaterais II¶
Na aula de hoje iremos trabalhar com um algoritmo de sorteios aleatórios para calcular o pi. Ele é baseado em uma técnica de Otimização, Simulação e Estimação Paramétrica chamada Monte Carlo. Um bom vídeo para compreender essa técnica, está disponível aqui.
O algoritmo sequencial se baseia em sorteios de pontos dentro de um quadrado de lado 2. Se a distância entre o ponto e o centro do quadrado for menor que 1 então o ponto cai dentro do círculo inscrito no quadrado. A quantidade de pontos que caem dentro do quadrado é proporcional a \pi. Veja abaixo um resumo do algoritmo.
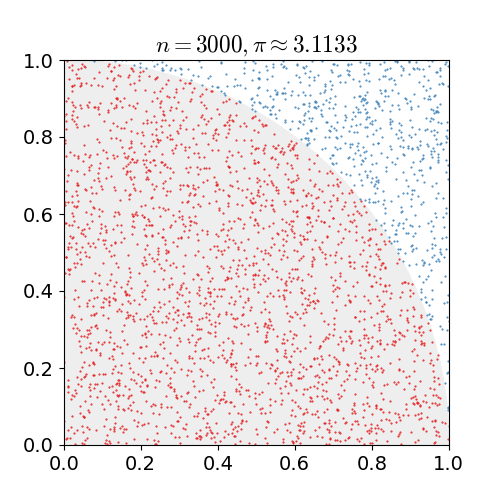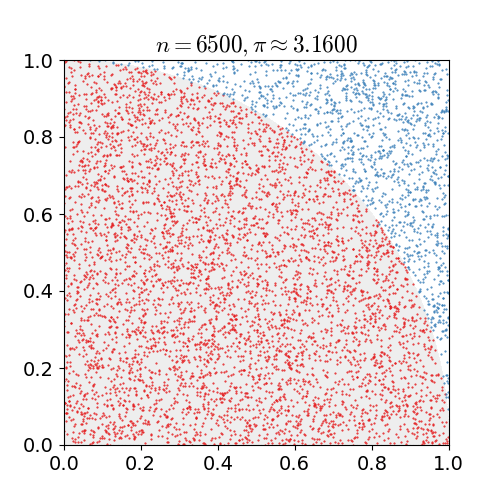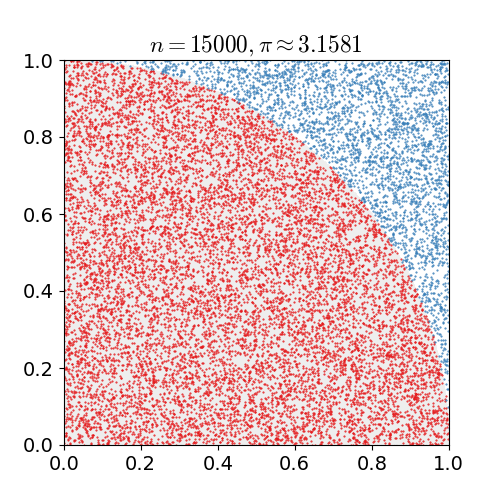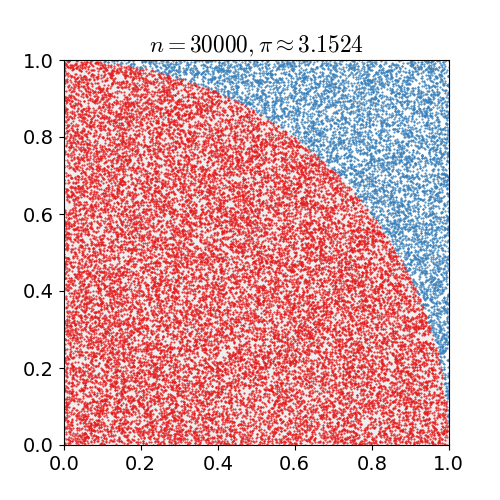
sum = 0- De
i=0atéN:- sorteie pontos x,y \in [0,1]
- se x^2 + y^2 \leq 1,
sum += 1
- devolva
4 * sum / N
Example
Faça uma implementação sequencial desse algoritmo. Chama seu programa de pi_montecarlo.cpp. Para fins de debug das próximas versões, mostre o valor de sum na saída de erros. Adote N=100 000.
É possível paralelizar o problema?¶
Vamos iniciar pensando um pouco sobre o problema acima.
Question
O algoritmo acima é paralelizável? Qual técnica você utilizaria para paralelizá-lo?
Resposta
O for paralelo parece encaixar muito bem neste problema, com a variável sum sendo usada na opção reduction
Question
Além da variável sum, existe outra operação que gera efeitos colaterais no código acima? Qual?
Resposta
O sorteio de pontos! Lembramos da aula 06 que a geração de números aleatórios é um processo sequencial que depende dos números anteriormente sorteados.
Progress
Continuar
Agora que sabemos que gerar números aleatórios é um processo sequencial, vamos considerar o quanto isso atrapalha nosso programa. Nas próximas questões leve em conta que o gerador de números aleatórios é uma variável compartilhada.
Question
Como evitaríamos problemas ao compartilhar o gerador de números aleatórios?
Resposta
Podemos envolver o passo 2a do algoritmo em uma seção crítica usando omp critical
Question
Se o for acima rodar em uma ordem completamente diferente os resultados se alterarão?
Resposta
Desde de que os pares x,y sorteados sejam os mesmos então não haverá problema.
Example
Com base em todas as suas respostas dos exercícios anteriores, faça uma implementação paralela do pi_montecarlo.cpp. Verifique que o valor de sum é igual ao sequencial. Por enquanto, não se preocupe com o tempo de execução.
Question
Anote o tempo de execução sequencial e paralelo para o programa acima.
Progress
Vamos discutir esse resultado juntos!
Paralelizando processos inerentemente sequenciais¶
Como discutimos agora há pouco, a geração de números aleatórios é um processo inerentemente sequencial. Não é que seja impossível paralelizá-lo eficientemente, é que é impossível paralelizá-lo at all. Vamos tentar contornar isso então usando a resposta da Questão 4:
O for do algoritmo depende dos pontos gerados, não da ordem que eles foram gerados.
Vamos então adotar uma solução simples: a cada iteração do for criamos um novo gerador de números aleatórios e sorteamos um par de pontos dele.
Primeira tentativa¶
Question
Sabemos que um gerador de números aleatórios gera sempre a mesma sequência de números, dado um parâmetro seed fixo. O quê acontece se usarmos o mesmo seed em todas as iterações? Como consertar isso?
Resposta
Sortearemos o mesmo ponto em todas as iterações. Para consertar isso podemos fazer o seed ser baseado no i da iteração atual.
Example
Crie uma implementação baseada na ideia acima.
Question
Anote abaixo o valor do pi encontrado e o tempo de execução.
Question
Os resultados obtidos são idênticos aos do programa original? São próximos?
Progress
Vamos discutir esse resultado.
Segunda tentativa¶
O problema da nossa tentativa anterior é que não temos de verdade sequências de pontos aleatórias. Bom, na verdade nunca temos, mas o problema é que violamos a promessa que o RNG faz. Ele promete que
dado um seed fixo, a sequência de números geradas é indistinguível de uma sequência aleatória de verdade
Ele não promete que, se criarmos vários RNGs, a sequência formada pelo primeiro par de números gerados por cada um será aleatória.
Vamos agora tentar uma nova ideia:
Cada thread irá gerar N/NUM_THREADS números aleatórios, atualizando sum com os pontos dentro do semi-círculo.
Question
Como esta ideia melhora o algoritmo acima?
Resposta
Agora teremos NUM_THREADS sequências pseudo-aleatórias "válidas" e juntá-las passa a ser um problema menor. Continuamos precisando usar uma seed para cada, mas ao menos agora temos um número pequeno de RNGs.
Example
Faça uma implementação da ideia acima. Você pode usar os comandos do OpenMP que quiser.
Question
Anote o tempo de execução e o pi encontrado.