Aula 2: medidas-sumário#

Objetivo da aula: ao fim desta aula, o aluno será capaz de usar medidas-sumário (média, desvio padrão, mediana, percentis) e as figuras correspondentes (histogramas, box plot) para evidenciar características de um conjunto de dados

Texto introdutório#

É comum lermos ou ouvirmos comparações como “alguns anos atrás, o mundo era mais tranquilo”, ou “as coisas estão piorando”. Essas impressões são importantes, mas nem sempre correspondem a dados reais. Na verdade, entender o comportamento de fatores sócio-econômicos como o acesso à renda, à educação e à saúde é muito importante para planejamentos nacionais e internacionais relacionados à aplicação e à avaliação de políticas públicas.

Usando a base de dados do Banco Mundial, temos acesso a vários indicadores sócio-econômicos de todos os países. Como temos acesso aos dados de todos os países possíveis, dizemos que esses dados se referem à população de todos os países (importante: não se tratam dos habitantes dos países, mas sim a população de todos os elementos que fazem parte do conjunto “países”). Com esses dados, podemos visualizar e entender melhor como o mundo de hoje se compara com o mundo de anos atrás.

Exercício 1#

Objetivo: entender dados do Banco Mundial

Abra no Excel o arquivo csv com dados de PIB per capita por país do Banco Mundial.

  1. Quantas linhas de cabeçalho existem no arquivo?

  2. Por que algumas linhas estão incompletas?

Exercício 2#

Objetivo: abrir dados do Banco Mundial em um dataframe e isolar as colunas de interesse

O trecho de código abaixo tenta abrir o arquivo com dados do Banco Mundial, mas retorna um erro.

  1. Que erro é esse e por que ele está acontecendo?

  2. Corrija o erro e confirme que os dados foram carregados.

  3. Use o método .loc (veja o tutorial em vídeo!) para encontrar o PIB per capita do Brasil em 2010.

import pandas as pd

df = pd.read_csv('dados/WorldBank/API_NY.GDP.PCAP.CD_DS2_en_csv_v2_3731360.csv', skiprows=4)
df.head()
Country Name Country Code Indicator Name Indicator Code 1960 1961 1962 1963 1964 1965 ... 2012 2013 2014 2015 2016 2017 2018 2019 2020 Unnamed: 65
0 Aruba ABW GDP per capita (current US$) NY.GDP.PCAP.CD NaN NaN NaN NaN NaN NaN ... 24712.493263 26441.619936 26893.011506 28396.908423 28452.170615 29350.805019 30253.279358 NaN NaN NaN
1 Africa Eastern and Southern AFE GDP per capita (current US$) NY.GDP.PCAP.CD 147.612227 147.014904 156.189192 182.243917 162.347592 180.214908 ... 1736.166560 1713.899299 1703.596298 1549.037940 1431.778723 1573.063386 1574.978648 1530.059177 1359.618224 NaN
2 Afghanistan AFG GDP per capita (current US$) NY.GDP.PCAP.CD 59.773234 59.860900 58.458009 78.706429 82.095307 101.108325 ... 638.845852 624.315455 614.223342 556.007221 512.012778 516.679862 485.668419 494.179350 516.747871 NaN
3 Africa Western and Central AFW GDP per capita (current US$) NY.GDP.PCAP.CD 107.932233 113.081647 118.831107 123.442888 131.854402 138.526332 ... 1965.118485 2157.481149 2212.853135 1894.310195 1673.835527 1613.473553 1704.139603 1777.918672 1710.073363 NaN
4 Angola AGO GDP per capita (current US$) NY.GDP.PCAP.CD NaN NaN NaN NaN NaN NaN ... 5100.097027 5254.881126 5408.411700 4166.979833 3506.073128 4095.810057 3289.643995 2809.626088 1776.166868 NaN

5 rows × 66 columns

Exercício 3#

Objetivo: usar o seaborn para plotar um histograma para visualizar distribuições

Um histograma é um tipo especial de gráfico de barras. A altura de cada barra corresponde ao número de elementos no conjunto cujo valor está em um determinado intervalo.

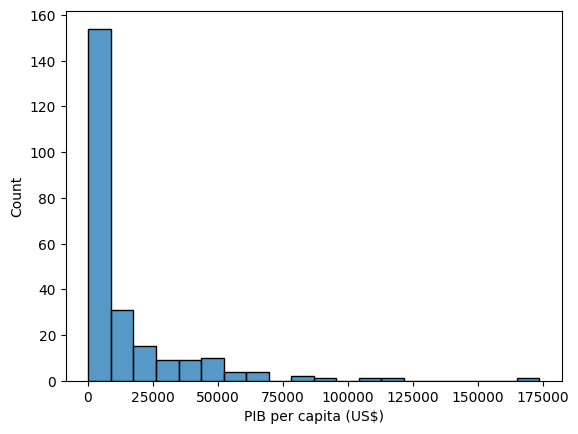
  1. Qual é o típico PIB per capita de países em 1990?

  2. O que acontece se modificarmos o valor do parâmetro “bins”?

  3. Modifique o código para mostrar o histograma do PIB per capita em 2020.

import matplotlib.pyplot as plt
plt.style.use('default')
import seaborn as sns

gdp = df['2020']

plt.figure()
sns.histplot(data=gdp, bins=20)
plt.xlabel('PIB per capita (US$)')
plt.show()
_images/cff7ffe700689a45c1378edde13a8896c78fd5e4cd2b9259239b0bf036e945e3.png

Exercício 4#

Objetivo: desenhar histogramas com diversos conjuntos de dados para evidenciar diferenças entre eles

Uma vantagem de usar figuras é que elas permitem visualizar diferenças entre dados. Para evidenciar diferenças, é importante colocar lado a lado os elementos que queremos diferenciar.

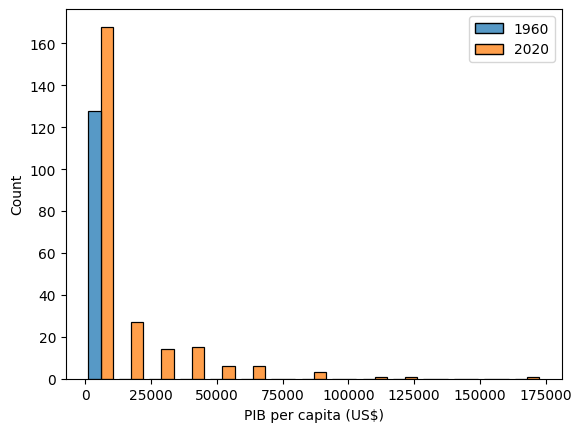
  1. No histograma gerado pelo código abaixo, o que podemos dizer sobre o que aconteceu com o PIB per capita no mundo entre 1960 e 1970?

  2. Que tipo de construção é usada para selecionar várias colunas de um dataframe?

  3. Modifique o trecho de código e verifique o que aconteceu com o PIB per capita no mundo década a década.

  4. Até quantas cores você consegue colocar no gráfico e ainda visualizar os resultados tranquilamente?

import matplotlib.pyplot as plt
plt.style.use('default')
import seaborn as sns

gdp = df[['1960','2020']]

plt.figure()
sns.histplot(data=gdp, bins=15, multiple="dodge", shrink=0.8)
plt.xlabel('PIB per capita (US$)')
plt.show()
_images/7bea492844fdafc3862fc6cb5686fcff617d089efaebee867024f48009e4e2fd.png

Exercício 5#

Objetivo: calcular a média de um conjunto de dados para evidenciar como o conjunto se comporta

A média é o valor que obtemos quando somamos todos os valores de um conjunto de dados e dividimos pelo número de elementos desse conjunto. Por exemplo, a média de \({1, 2, 3, 4}\) é \( (1+2+3+4) / 4 = 10/4 = 2.5\).

O trecho de código abaixo mostra como calcular a média de uma coluna de um dataframe.

Faça uma figura mostrando como a média do PIB per capita de todos os países do mundo se comportou desde 1960 até 2020.

gdp_medio = df['1960'].mean()
print(gdp_medio)

482.72531432586766

# Faça sua figura aqui

Exercício 6#

Objetivo: calcular a mediana de um conjunto de dados para evidenciar como o conjunto se comporta

A mediana é um outro valor que indica a centralidade de um conjunto de dados. Ela é calculada da seguinte forma: os valores do conjunto são ordenados do menor para o maior, e a mediana é o valor correspondente ao elemento central dessa lista.

  1. Qual é a mediana do conjunto: \({4, 2, 5, 3, 1}\)?

  2. No conjunto acima, se trocarmos o elemento \(5\) por \(50\), quem seria mais afetado: a média ou a mediana?

  3. Qual medida (média ou mediana) se refere à expressão “países, em média”? E qual se liga a “o país médio”?

  4. O trecho de código abaixo mostra como calcular a mediana de uma coluna de um dataframe. Crie um plot que mostra a mediana do PIB per capita de países ao longo dos anos entre 1960 e 2020.

gdp_mediano = df['1960'].median()
print(gdp_mediano)

197.897848206733

# Faça sua figura aqui

Exercício 7#

Objetivo: calcular o desvio padrão de um conjunto de dados para entender sua dispersão

O desvio padrão é uma medida de dispersão, isto é, valores maiores do desvio padrão significam que as medidas estão mais “espalhadas”. Ele é calculado como a média do quadrado da diferença em relação à média, ou:

\[\begin{split} \mu = \frac{\sum_{n=1}^{N} x_n}{N}\\ \\ \\ \sigma = \sqrt{\frac{\sum_{n=1}^{N} (x_n-\mu)^2}{N}} \end{split}\]

O desvio padrão significa a diferença esperada entre um elemento qualquer e a média da população. Isso significa que, por exemplo, que se a média de notas de uma população de alunos for 8 e o desvio padrão for 2, então uma pessoa que tirou 7 está a meio desvio padrão da média, o que está dentro do desvio tipicamente esperado. Porém, se o desvio padrão for 0.5, então essa pessoa que tirou 7 está dois desvios padrões longe da média, o que significa uma diferença bem mais atípica.

O código abaixo permite calcular o desvio padrão de uma coluna de um dataframe.

  1. Faça uma figura mostrando como o desvio padrão do PIB per capita se comporta ao longo do tempo.

  2. Faça uma figura mostrando como a razão entre o desvio padrão e a média do PIB per capita se comporta ao longo do tempo.

gdp_std = df['1960'].std()
print(gdp_std)

626.040167865528

Exercício 8#

Objetivo: calcular percentis para evidenciar a dispersão em medidas

Uma outra medida de dispersão é o percentil. O x-percentil, ou percentil x, é o valor abaixo do qual está \(x\%\) de seu conjunto. O raciocínio é semelhante ao da mediana. Na verdade, o percentil 50 é exatamente a mediana.

Um quantil é exatamente o mesmo, exceto que ao invés de medir quantidades em porcentagens elas são medidas em frações, isto é, a mediana é o quantil \(0.5\).

O código abaixo permite calcular um quantil de uma coluna.

Existe uma frase muito comumente falada, que é:

Apesar do progresso mundial, os países pobres se tornaram ainda mais pobres nos anos mais recentes

Em contraposição a ela, outras pessoas respondem:

Os países pobres estão muito menos pobres do que já estiveram! O mundo está evoluindo para todos!

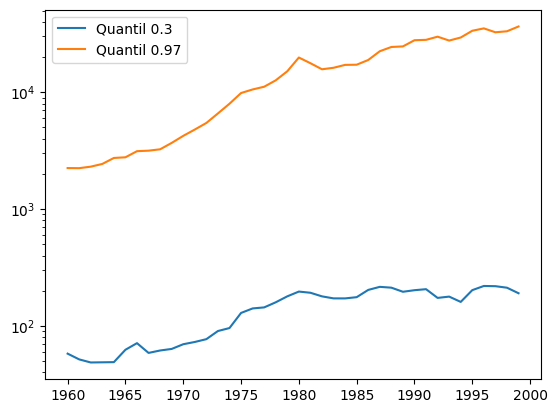
  1. Faça uma figura que permita comparar a evolução do PIB per capita nos 3% países mais pobres com a evolução nos 3% mais ricos. Dica: como estamos falando de variações de grandezas, pode ser útil usar o eixo y em escala logaritmica com plt.semilogy().

  2. Pela sua figura, como você analisaria as duas frases colocadas acima?

gdp_qnt = df['1960'].quantile(q=0.7)
print(gdp_qnt)

429.4240015605796

ano = range(1960,2000)
gdp_pob = []
gdp_ric = []

for a in ano:
    gdp_pob.append(df[str(a)].quantile(q=0.03))
    gdp_ric.append(df[str(a)].quantile(q=0.97))

plt.figure()
plt.plot(ano, gdp_pob, label='Quantil 0.3')
plt.plot(ano, gdp_ric, label='Quantil 0.97')
plt.legend()
plt.semilogy()
plt.show()
_images/b434eb8f1cef8b3fd6dac54f05e0401edeb87c60df61acb67ac4dfae19fe98c8.png

Exercício 9#

Objetivo: plotar e interpretar boxplots

Um boxplot é um tipo de figura muito comum em estatística que mostra a dispersão de um conjunto de dados. Tipicamente, ele marca a mediana e os quantis \(0.25\) e \(0.75\).

A diferença entre os quantis \(0.75\) e \(0.25\) é chamada de Inter-Quartile Range (IQR). Elementos cuja distância a um quartil é maior que \(1.5 \times \text{IQR}\) são considerados outliers.

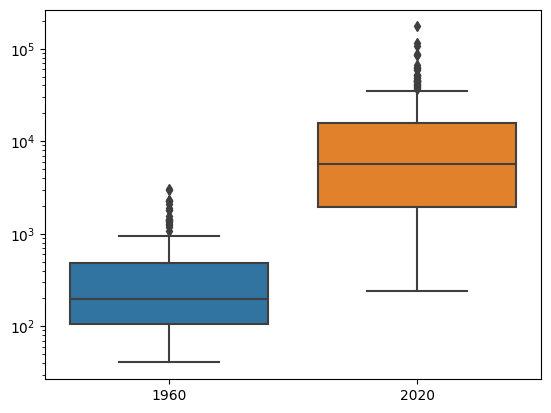
O código abaixo mostra como fazer um boxplot dos dados de PIB per capita. Modifique o código para mostrar o que está acontecendo com o PIB per capita dos países a cada década desde 1960.

plt.figure()
sns.boxplot(data=df[['1960', '2020']])
plt.semilogy()
plt.show()
_images/973331f508e0be72ce33edf951e0c5cd59de2956346c6db1eb90d58c35dc9898.png

Exercício 10#

Objetivo: encontrar países em ascenção

É possível calcular valores à partir de colunas de um dataframe - veja este tutorial em vídeo.

Um indicador de sucesso de um país é o crescimento relativo de seu pib. Para calcular o crescimento relativo do PIB entre 2000 e 2010, por exemplo, podemos usar a fórmula:

\[ \Delta \text{PIB} = \frac{\text{PIB}_{2010}-\text{PIB}_{2000}}{\text{PIB}_{2000}} \]

Usando essas informações, responda: dos países ativos do Mercosul (Argentina, Brasil, Paraguai e Uruguai), qual teve o maior crescimento relativo entre os anos de 1991 (data de criação do Mercosul) até 2020?

Exercício 11#

Objetivo: aplicar as medidas-sumário para analisar dados de indicadores do World Bank e evidenciar alguma informação importante em relação ao mundo

O Banco Mundial disponibiliza um conjunto grande de indicadores relacionados a países. Muitos deles permitem posicionar-se, com base em dados, frente a temas como desnutrição, equidade de gênero, educação, poluição, etc. Em especial, com as técnicas que aprendemos nesta aula, podemos entender como os dados se comportam ao longo do tempo para os diversos países do mundo.

  1. Navegue pela base de dados do Banco Mundial. Escolha um indicador para responder à pergunta: “o número de pessoas com acesso a instalações de saneamento básico tem diminuído”.

  2. Baixe os dados e certifique-se de que eles estão completos o suficiente para responder à sua pergunta.

  3. Usando as técnicas que aprendemos hoje, faça uma figura que evidencie a resposta à sua pergunta.

  4. Não esqueça de rotular eixos e colocar título na figura! No título, tanto a pergunta quanto a resposta devem ficar evidentes.