09 - Correlações#
Objetivo da aula: ao fim desta aula, o aluno será capaz de encontrar correlações entre variáveis para gerar decisões e planejamentos baseados em evidências.
import pandas as pd
import matplotlib.pyplot as plt
plt.style.use('default')
import seaborn as sns
Texto introdutório#
Em muitas situações, dizemos que “quanto mais X, mais Y”. Um exemplo disso é quando pensamos que “quanto mais tempo de estudo, melhor o desempenho na prova”. Para fins de exemplo, inventei os dados abaixo:
df = pd.DataFrame()
df['Tempo de estudo (h)'] = [1.5, 2.2, 3, 4, 3, 2, 2, 1, 4]
df['Nota na prova'] = [5, 6, 7,7, 8, 6, 6.5, 4.5, 8]
plt.figure(figsize=(2,2))
sns.scatterplot(data=df, x='Tempo de estudo (h)', y='Nota na prova')
plt.show()
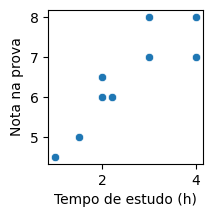
O gráfico que foi desenhado na tela é um “gráfico de espalhamento”, ou “scatterplot”. Nele, cada ponto é um aluno, e sua posição indica o tempo de estudo (no eixo X) e a nota na prova (eixo Y). Veja que, embora os pontos não formem uma reta perfeita, eles se parecem mais com uma reta que se fossem pontos aleatórios!
A força dessa associação do crescimento de uma variável ao crescimento da outra variável é chamado de correlação. A correlação é calculada por:
$\( r_{xy} = \sum_{i=1}^N \frac{ (x_i-\mu_x) (y_i-\mu_y) }{N \sigma_x \sigma_y} \)$, onde:
\(N\) é o número de elementos nas séries \(x\) e \(y\) .
\(\mu_x\) e \(\mu_y\) representam as médias das séries \(x\) e \(y\),
\(\sigma_x\) e \(\sigma_y\) representam os desvios padrões das séries \(x\) e \(y\)
Embora a equação seja essa, nós não a implementaremos manualmente. Ao invés disso, usaremos pandas para gerar um novo DataFrame que contém as correlações que queremos:
rxy = df.corr()
print(rxy)
print( "Correlação:", rxy.loc['Nota na prova']['Tempo de estudo (h)'])
Tempo de estudo (h) Nota na prova
Tempo de estudo (h) 1.000000 0.875608
Nota na prova 0.875608 1.000000
Correlação: 0.8756084675952558
A correlação pode assumir valores entre 1 e -1. Se está próxima de 1, significa que a associação é forte e quando um fenômeno aumenta, o outro também aumenta. Se é próxima de -1, a associação também é forte, mas, quando um fenômeno aumenta, o outro diminui. Se está próxima de zero, isso significa que as variáveis medidas têm associação fraca, ou que são descorrelacionadas. Embora haja alguns manuais com níveis de correlação e possíveis interpretações, o uso adequado desta ferramenta depende do contexto em que a interpretação é feita.
Sob um ponto de vista estritamente científico, temos as seguintes situações:
Se \(r_{xy}\) está próximo de 1 ou -1, é possível que haja algum tipo de associação entre os fenômenos medidos.
Se \(r_{xy}\) está muito próximo de 0, então seus dados indicam que não há nenhum tipo de associação entre os fenômenos medidos.
Exercício 1#
Objetivo: usar scatterplot e correlação para julgar uma hipótese
Usando um scatterplot e uma medida de correlação, use dados do Banco Mundial para discutir a seguinte afirmação:
Os países que são mais ricos em 2020 são os mesmos países que já eram os mais ricos em 1980!
# Resolva seu exercício aqui
df_pib_per_capita = pd.read_csv('dados/WorldBank/API_NY.GDP.PCAP.CD_DS2_en_csv_v2_3731360.csv', skiprows=3)
Exercício 2#
Objetivo: usar dados de múltiplas tabelas para discutir uma hipótese
O desmatamento é um problema ligado ao desenvolvimento sustentável de países. É comum ouvirmos dizer que os países mais ricos do mundo já devastaram suas próprias florestas e, portanto, o desmatamento é um caminho inevitável para o progresso de um país.
Os dataframes abaixo carregam dados do Banco Mundial referentes ao PIB per capita e à porcentagem de área coberta por florestas de cada país.
O problema agora é que temos dados relevantes, relacionados aos mesmos países, mas em dataframes diferentes! Por isso, será necessário usar o método merge (veja o tutorial em vídeo aqui).
Use esses dados para gerar um scatterplot e calcular correlações para discutir a hipótese:
Em 2020, quanto mais rico é um país, menor é sua área coberta por florestas
df_area_florestal = pd.read_csv('dados/WorldBank/API_AG.LND.FRST.ZS_DS2_en_csv_v2_3731376.csv', skiprows=3)
df_pib_per_capita = pd.read_csv('dados/WorldBank/API_NY.GDP.PCAP.CD_DS2_en_csv_v2_3731360.csv', skiprows=3)
Exercício 3#
Objetivo: comparar correlações de analisar hipóteses sobre diferentes comportamentos
Podemos argumentar que a análise feita no exercício 2 é incompleta porque considera apenas um ano. Talvez o que tenha acontecido é que os países que já eram cheios de florestas continuaram cheios de florestas e os que não tinham florestas continuaram assim, ou talvez os países ricos tenham simplesmente tido mais recursos para reflorestar seus territórios. Por isso, deveríamos analisar os dados históricos relacionando PIB per capita e taxa de florestamento para cada país.
Para cada país em nosso conjunto de dados, calcule a correlação entre o PIB per capita e a área florestada.
Faça um histograma das correlações encontradas e calcule sua média e desvio padrão. Quais são os comportamentos típicos encontrados?
Faça a mesma análise, agora comparando os 20% de países mais pobres aos 20% mais ricos. Quais são as diferenças evidenciadas?
Faça a mesma análise, agora comparando os 20% de países mais cobertos de florestas aos 20% menos cobertos de florestas. Quais são as diferenças evidenciadas?
df_area_florestal = pd.read_csv('dados/WorldBank/API_AG.LND.FRST.ZS_DS2_en_csv_v2_3731376.csv', skiprows=3).set_index('Country Name')
df_pib_per_capita = pd.read_csv('dados/WorldBank/API_NY.GDP.PCAP.CD_DS2_en_csv_v2_3731360.csv', skiprows=3).set_index('Country Name')